The Circle-Ellipse Problem is a modeling failure in object-oriented programming that is the result of a number of misunderstandings and incorrect assumptions about the modeling domain and about subtyping relationships. Applying accepted software design principles exposes several problems in the circle-ellipse problem and indicates how the problem can be avoided altogether.
The Circle is-a Ellipse parent/child class relationship is stated as a premise. The hypothesis is that it is also a subtyping relationship. A faulty conclusion is reached that demonstrates a modeling contradiction.
In this article I will use the term is-a for any subtyping relationship even where is-an would be the grammatically correct term.
The Circle-Ellipse Problem Statement
The ellipse shown below is bisected in two ways, once by the AB major axis and once by the CD minor axis.
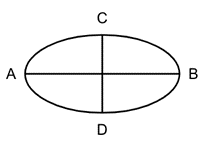I will call the length of the AB axis the X property of the ellipse, and the length of the CD axis the Y property of the ellipse.
When the X and Y properties are not equal the shape is said to be an ellipse.
When the X and Y properties are equal, the shape is said to be a circle.
Let us create an Ellipse class to model these ellipse objects, and give the class two member variables X and Y corresponding to the X and Y properties of the ellipse, and two methods stretchX and stretchY that allow modification of an Ellipse instance’s X and Y member variables.
Now we create an Ellipse subclass called Circle. It inherits the stretchX and stretchY methods.
Calling one of those stretchX or stretchY methods on a Circle instance creates a problem because it stretches the Circle instance so that it represents a shape that is no longer circular.
Hereafter in this article, there is no need to distinguish between the two stretchX and stretchY methods in the Ellipse class and I will refer to them collectively as a single stretch method.
I did my best to reproduce the problem statement above even though I reworded it a bit, but you should read the Wikipedia article for yourself.
The Circle is-a Ellipse Relationship
It is generally accepted that the Circle is-a Ellipse relationship is modeled after the Euclidean geometry. The Wikipedia article on the Ellipse indicates that the ellipse “… generalizes a circle, which is the special type of ellipse in which the two focal points are the same.”
That sounds like there ought to be a subclassing relationship.
Focal Points and Directrices
Below is a graphical representation of how an ellipse can be constructed. In the diagram there are two focal points, and the dotted line segments are called directrices, where each line segment is a single directrix.
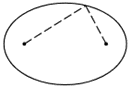
If the lengths of the directrices are allowed to vary but the sum of the lengths of the directrices is held to a specific constant value, then the places where the endpoints of the directrices intersect are all the points in the set that make up the ellipse. This is the locus of the ellipse. The ellipse is this locus.
The closer the two focal points are, the less elongated and more circular the ellipse becomes.
If the distance between the focal points is 0 then the shape forms a circle, and this is often said to be a special case or a degenerate case of the ellipse.
So if bringing the focal points together makes a circle, what happens if the focal points are spread apart? The ellipse flattens as the focal points become more distant. When the distance between the focal points equals the sum of the lengths of the directrices, the shape forms a line segment. Thus the line segment is also a degenerate case of the ellipse when this specific construction method is used.
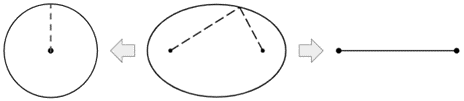
If the distance between the focal points is 0 and the lengths of the directrices are also 0, then this is yet another degenerate case that forms a point.
Furthermore it is possible to describe an ellipse using a number of different equations, where the circle, the point, and the line segment are also degenerate cases of each.
Thus if one considers all the degenerate cases of each of these methods of creating an ellipse, one must also consider not only circles but also lines and points.
If you argue that a circle is a special kind of ellipse, then you must also agree that a line and a point are also each a special kind of ellipse.
The Constructor is not the Object
What’s crucial to understand, though, is that any superclass/subclass relationship between an ellipse and a circle applies only to the means of describing or constructing those shapes, but not to the shapes themselves. The equations, or the foci and directrices, are used to create the ellipse but they are not components of an ellipse. The shape is not the process used to create the shape, the shape is the locus of points that is the result of the process. The shape is not the equation that describes the shape, the shape is the locus of points that manifests from the equation.
Conic Sections
The diagram below kindly taken from the Wikipedia page on conic sections shows another way that a circle and an ellipse can each be defined:
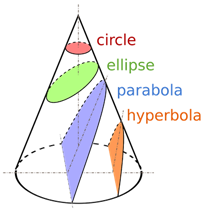
● A circle is that shape described by the locus of points that is the intersection of a cone with a plane when that plane is parallel to the base of the cone.
● An ellipse is that shape described by the locus of points that is the intersection of a cone with a plane when that plane is not parallel to the base of the cone.
The property that distinguishes a circle from an ellipse is the angle with which the plane intersects the cone relative to the cone’s base. For a circle that angle is 0. For an ellipse that angle is not 0. There is no overlap. In a proper subtyping relationship the subtype is a set that is fully contained in the set that defines the supertype, but the mathematical intersection between the set of circles and the set of ellipses created from conic sections is the empty set.
It is not correct to argue that there is one circle while there are many ellipses. The set of all circles is an uncountably infinite set, as the cone extends to infinity. The set of ellipses is also infinite. The cardinality of the set if ellipses is infinity × infinity: there’s one uncountable infinity (called aleph-one, or ℵ1) representing all the locations where each ellipse intersects the infinite cone, and there’s another uncountable infinity for the infinite number of possible angles (even though the range of angles must be clamped to prevent the ellipse from forming a parabola or a hyperbola — a subset of ℵ1 is still ℵ1), but the product of two uncountable infinities (ℵ1 × ℵ1) is still just the same uncountable infinity ℵ1. Thus, the sizes of the set of all circles and the size of the set of all ellipses are the same. The cardinality of these two sets alone shows that neither set can be a proper subset of the other.
Regardless of the number of circles and ellipses, what is not shown in the diagram above is the case where the plane intersects the cone at the cone’s apex at some small angle relative to the base of the cone (where the plane is balanced flat on the tip of the cone). This forms a point.
Another case is where the plane intersects the cone at the apex with an angle equal to the cone’s vertex angle (where the plane is resting along the side of the cone). This forms a line, and this time it’s a line rather than a line segment.
Thus when we consider conic sections, it is still possible to use the same construction mechanism to create an ellipse, circle, point, and line. But since we are using conic sections as the construction mechanism we must now also consider a parabola and a hyperbola.
Each of the conic sections can be described as a more specific version of another, just with a slight mutation of properties: An ellipse is-a parabola that is closed. A parabola is-a hyperbola that intersects the cone only once.
Let’s try the reversals of those conic section relationships: A hyperbola is-a parabola that intersects the cone twice. A parabola is-a ellipse that isn’t closed. A parabola is-a circle that’s stretched. So which is it? Is an ellipse a kind of circle or is it a kind of parabola? It can be either because the is-a relationship is an axiomatic statement of intent that is not subject to falsification. It is not a theorem supported by evidence.
I could just as easily proclaim that a square is-a circle that has four right angles, or a circle is-a square with the right angles removed, or a circle is-a polygon with an infinite number of sides. Subclassing based on properties instead of behaviors allows us to establish any is-a subclassing relationship at all, whether or not it is a valid subtyping relationship.
No conic section is a proper subtype of any other conic section.
Issues with the Circle-Ellipse Problem
These are a few easily-identifiable problems with the circle-ellipse problem.
-
- Circle is-a Ellipse is a bijection violation.
If you’re not already familiar with the bijection principle of software design then I encourage you to read that article right away.The Euclidean geometry makes no provision for a circle to be a kind of ellipse. This was detailed in the previous section.
It is possible to assert the subclassing relationship Circle is-a Ellipse, but understand that this is an axiomatic and unfalsifiable relationship that is not automatically a subtyping relationship.
It is a mistake to consider a circle to be a kind of ellipse in Euclidean geometry, and it is a bijection violation to model that class relationship.
- The Ellipse class is incorrectly assumed to have behaviors.
The Euclidean geometry is static. Shapes in Euclidean geometry have properties that are their defining and identifying characteristics but they do not have behaviors.
- The Circle and Ellipse classes are incorrectly placed in a subclassing relationship.
The subclassing relationship is incorrect for two reasons, the first of which was shown in the previous section on conic sections.
Since the set of behaviors for each of the Circle and Ellipse classes is empty, then the set of behaviors for both classes is the same. I will discuss adding behaviors to these classes in a later point below.
Applying the Liskov Substitution Principle (LSP) to the Circle is-a Ellipse relationship reveals that it is a valid subtyping relationship. This works because the Ellipse class has no behaviors that can be violated.
But what is interesting is that applying LSP to the reverse Ellipse is-a Circle relationship reveals that this is also a valid subtyping relationship.
Thus equal or empty sets of behaviors result in a reflexive subtyping relationship, so neither is a proper subtype of the other. It is not correct to make one class a subclass of the other for the purposes of subtyping or modeling since both relationships are valid and neither relationship can be invalidated.
On the one hand the classes could be considered to be unrelated, but on the other hand drawing from our domain knowledge of Euclidean geometry it is quite reasonable to allow the Circle and Ellipse classes to be siblings with a common superclass called Shape.
- Giving the Ellipse class mutable properties and a setter function is a bijection violation.
The Euclidean geometry makes no provision for a shape to have mutable properties, so giving a shape model mutable properties is a bijection violation.
In Euclidean geometry, properties and identity are inextricably linked. To change the properties of a shape is to change its identity. An ellipse that is “mutated” so that it becomes circular changes its identity from an ellipse into a circle. An ellipse that is “stretched” or “squashed” enough to become linear changes its identity from an ellipse into a line segment. The ellipse or line segment can be further “shortened” until it changes its identity to be a point. Any line segment can be “expanded” into an ellipse or a circle, or it can even be “bent” into a parabola.
The Euclidean geometry makes no such provision for any of these imaginary mutations. Even when mutating a shape into the same type of shape (like “changing” the radius of a circle) the two shapes are not the same shape. The new shape represents a locus of points that is not the same as the original locus of points.
- The Ellipse’s stretch method is incorrectly assumed to be a behavior.
To be stretchable is not a behavior inherent in a shape. Stretching is something that is done by another entity and not by the shape itself.
Furthermore, a stretch behavior is nothing more than a property-mutating function, which we typically call a setter. A setter is not a behavior, it is a mutable property masquerading as a function (although we might say that it’s half a mutable property, where the other half would of course be the associated getter).
- The subclassing relationship in the circle-ellipse problem is incorrectly implied to be a subtyping violation.
The Circle subclass in the original statement of the circle-ellipse problem has no behaviors of its own, but even if we were to allow the stretch method in the Ellipse class to be an actual behavior, then the Circle class would inherit that behavior. Invoking that stretch method on a Circle instance would modify the properties of that instance accordingly but that Circle instance would still behave as if it were an instance of the Ellipse superclass. The only subtyping behavior is the stretch method, which still works as it should for any Circle instance.
Thus not only is the circle-ellipse problem not a subtyping violation (at least not as the problem is stated, but I will address this below), but LSP can be used to validate this relationship. Circle is-a Ellipse (so far) is still a valid subtype relationship.
- LSP is misapplied to the Circle subclass.
LSP makes no claim about the behavior of a subclass instance with regard to its own class, only with regard to the instance’s superclass.
The circle-ellipse problem article states that “the problem illustrates the difficulties which can occur when a base class contains methods which mutate an object in a manner which may invalidate a (stronger) invariant found in a derived class, causing the Liskov substitution principle to be violated.”
This invariant violation in the Circle class is a violation of neither behavioral subtyping nor of LSP. It is, however, a bijection violation: we expect our Circle instances to represent circular shapes using the properties we give them.
It doesn’t matter what invariant is found in a subclass. LSP is concerned only with the invariants found in the superclass. - Only by overriding the Ellipse class’s behavior can we create a subtyping violation.
LSP can’t be violated unless we override and change one or more of the superclass’s behaviors.
Let’s override the stretch method in the Circle class so that whenever a Circle instance is stretched along one axis (such as the major axis AB in the diagram below, making it elliptical as it is shown here), the instance automatically stretches itself along the perpendicular axis (minor axis CD in the image below) by an equal amount, thereby maintaining the circularity of the instance.
Even doing this the Circle class still does not violate behavioral subtyping because the Circle instance still behaves as a proper Ellipse. This is evidence to support the claim that a property-changing setter is not a behavior. There is currently no behavior in the Ellipse class that depends on an Ellipse instance to represent an elliptical object, so no behavior has been violated.We’re nearly there, though, I promise.
We must now add a behavior to the Ellipse class that depends on the distinction between a circle and an ellipse and this can be as simple as adding an area() method to the Ellipse superclass, and then claim that this is the behavior we care about (but be aware that area is actually a derived property getter and not truly a behavior, but it’s sufficient for our purposes here). Nevertheless, we can finally use LSP to show that a Circle instance that has been used as if it were an Ellipse, where it has been stretched and has re-circularized itself, will not have the area that you would expect if it had the properties of an Ellipse. This Circle instance finally violates the behavior of the Ellipse class.
Furthermore, there are additional bijection violations: The Ellipse class violates the Circle class’s invariant of being circular by attempting to force a Circle instance to be elliptical, and the Circle class violates the Ellipse class’s invariant of being elliptical by forcing an Ellipse instance to be circular.
- Circle is-a Ellipse is a bijection violation.
Conclusion
The Circle-Ellipse Problem highlights significant conceptual pitfalls in object-oriented programming, emphasizing the need for meticulous design and understanding of subclassing relationships. As software designers, it is imperative to challenge our assumptions and model relationships based on accurate behaviors rather than convenient hierarchies. If you found this discussion enlightening and seek further insights into robust software design practices, sign up for our new article alerts. Let’s build smarter, error-free software together!
Author: Jeff Meunier, Senior Software Engineer at Geisel Software
